Understanding Conditional Probability for beginner

In the modern era of data-driven decision-making, understanding probability is essential for professionals, students, and researchers alike. One crucial concept that often forms the backbone of statistical reasoning is conditional probability. For beginners, mastering this concept is critical, as it is widely used in fields such as machine learning, finance, healthcare, and risk analysis. 

This article delves into the fundamentals of conditional probability, its formula, practical examples, and its connection to Bayes conditional probability, conditional expectation, and real-world applications.

What is conditional probability?

Conditional probability refers to the likelihood of an event occurring given that another related event has already occurred. Unlike simple probability, which considers events independently, conditional probability allows us to refine our predictions based on additional information.

Mathematically, if we have two events, A and B, the conditional probability of event A occurring given that B has occurred is represented as P(A|B). This concept is critical in situations where events are dependent on one another. For example, the probability of drawing an ace from a deck of cards changes if we already know a face card has been drawn first.

Understanding conditional probability is not only essential in pure statistical analysis but also serves as a foundation for advanced topics like Bayes conditional probability, which allows the updating of probabilities based on new evidence, and conditional expectation, which predicts expected values under certain conditions.

The conditional probability formula

The conditional probability formula is the cornerstone of calculating probabilities for dependent events. It is defined as:

[ P(A|B) = {P(A \B)}*{P(B)} \P(B)  ]

Here:

• P(A|B) is the probability of event A occurring given that B has occurred.
• P(A ∩ B) is the probability that both events A and B occur simultaneously.
• P(B) is the probability of event B.

This formula allows us to quantify how the occurrence of one event influences the probability of another, which is especially useful in conditional probabilities examples such as:

• Probability in medical testing: In medical diagnostics, conditional probability helps determine the likelihood of a patient having a particular disease given a positive test result.
• Weather predictions using conditional probability: Meteorologists use conditional probability to estimate the likelihood of rainfall given certain observed conditions, such as a cloudy sky or high humidity.
• Determining market behavior: Investors and analysts apply conditional probability to assess the probability of a stock price increasing based on specific market trends or economic indicators. 

By applying the conditional probability formula, learners can approach complex real-world problems with a structured, mathematical framework.

Refer to the articles below:

• Categorical Analysis: Methods, Applications, and Insights
• Star Schema vs Snowflake Schema
• The Role of Data Quality in Digital Transformation

Introduction to Bayes’ Theorem

A critical extension of conditional probability is Bayes’ Theorem, often referred to as Bayes conditional probability. Bayes’ Theorem provides a method to update probabilities when new information becomes available. The theorem is expressed as:

[ P(A|B) = {P(B|A) \c* P(A)}{P(B)}, \ \ P(B)  ]

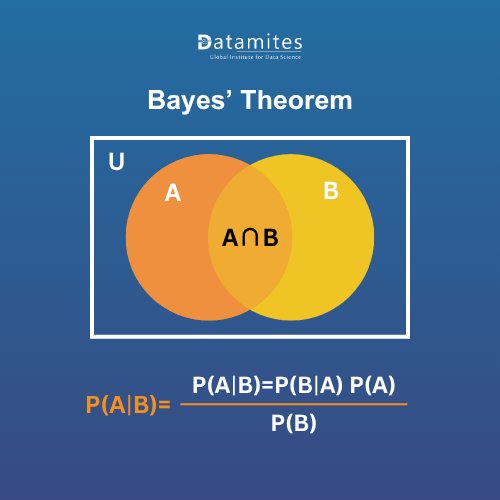
Here:

• P(A|B) is the updated probability of A given B.
• P(B|A) is the likelihood of observing B assuming A is true.
• P(A) is the prior probability of A.
• P(B) is the total probability of B occurring.

Bayes’ Theorem is a powerful statistical and data analyst tool with wide-ranging applications across various fields, enabling informed decision-making by updating probabilities based on new information. Bayes’ Theorem has numerous applications across disciplines:

• Used for analysis in healthcare: Bayes’ Theorem is widely used in medical diagnostics to calculate the probability of a patient having a particular disease given the results of medical tests. It helps doctors make informed decisions by combining prior knowledge about disease prevalence with observed test outcomes, improving diagnostic accuracy.
• Machine learning model for probability: In machine learning, Bayes’ Theorem forms the foundation of Naive Bayes classifiers, which are extensively used for tasks like spam email detection, sentiment analysis, and text classification. It allows models to predict the probability of a class given certain features, making it efficient for large datasets.
• Determining the trends in finance: Bayes’ Theorem assists financial analysts by using data analytics in finance in updating risk assessments and investment decisions based on new market information. By combining historical data with current trends, it provides a systematic approach to managing uncertainty in stock trading, credit scoring, and portfolio management.
• Quality control and inspection: In manufacturing and production, Bayes’ Theorem helps determine the probability of defects in a batch of products based on inspection results. This enables companies to optimize quality assurance processes and reduce waste by making data-driven decisions about production standards.
• Used in weather forecasting: Meteorologists use Bayes’ Theorem to improve the accuracy of weather predictions by updating the likelihood of events such as rain, storms, or temperature changes based on new observational data. It allows forecasters to refine predictions continuously as fresh information becomes available.

Understanding Bayes’ Theorem helps learners not just calculate conditional probabilities but also develop a deeper intuition for reasoning under uncertainty, an essential skill in analytics and data science.

Common Pitfall and Misconceptions of conditional probability

Despite its importance, beginners often make mistakes when applying conditional probability. Some common pitfalls include:

• Confusing P(A∣B)P(A|B)P(A∣B) with P(B∣A)P(B|A)P(B∣A): Many learners mix up the direction of the condition. P(A∣B)P(A|B)P(A∣B) means the probability of A happening given that B has occurred not the other way around. Switching these changes the meaning entirely.
• Ignoring the condition event: A frequent mistake is calculating P(A)P(A)P(A) directly instead of considering that B has already occurred. Always remember that conditional probability focuses only on the subset of outcomes where B is true.
• Forgetting to divide by P(B)P(B)P(B): Some beginners compute only P(A∩B)P(A \cap B)P(A∩B) but forget to divide by P(B)P(B)P(B). This step is essential it adjusts the probability based on the given condition.
• Assuming independence without checking: Learners sometimes assume events are independent and use P(A∣B)=P(A)P(A|B) = P(A)P(A∣B)=P(A) without verifying it. Independence must be proven or stated, otherwise, it leads to incorrect results.
• Misinterpreting “Given” as causation: Conditional probability shows association, not cause and effect. Just because B has occurred and we calculate P(A∣B)P(A|B)P(A∣B) doesn’t mean B causes A. Always interpret results carefully.

By being aware of these pitfalls, learners can approach conditional probabilities examples more confidently and avoid common mistakes in practical applications.

Applications of conditional probability across industries

Conditional probability is not just a theoretical concept; it has numerous real-world applications across diverse fields. Here are a few practical examples:

1. Healthcare and epidemiology: Calculating the likelihood of patients having a disease by adopting data analytics in healthcare based on symptoms or test results is an essential application of conditional probability. It is often combined with Bayes conditional probability for diagnostic accuracy.
2. Finance and risk analysis: Investors use conditional probability to assess risks and returns. For instance, the probability of a stock market dip given specific economic indicators helps in decision-making.
3. Machine Learning and artificial intelligence: Algorithms often use conditional expectation to predict outcomes. Naive Bayes classifiers, for instance, rely heavily on conditional probability for predicting and prescriptive analysis categories in datasets.
4. Used in quality control: Data analytics in Manufacturers evaluate defect probabilities conditional on production line events, ensuring quality assurance and reducing errors.
5. Used for weather forecasting: Meteorologists calculate conditional probabilities to predict weather patterns based on observed conditions, like humidity or cloud cover. 

The study done by Research Gate concludes that Bayes’ Theorem is highly effective for real-world decision-making across domains like healthcare and finance, improving prediction accuracy. For instance, a weather model showed a 33% probability of actual rain when a rain forecast was issued.

Through these applications, beginners can see how conditional probability bridges the gap between theory and practice, making it a vital tool in analytics, research, and decision-making processes.

Refer to the articles below:

• Data Analyst Course Fee in Pune
• Data Analyst Career Scope in Pune
• How to Become a Data Analyst in Pune

Conditional probability is a key statistical concept that helps evaluate the likelihood of an event based on given information. By learning the conditional probability formula, exploring examples, and applying Bayes conditional probability and conditional expectation, beginners can build strong analytical skills. Mastery of these concepts enhances decision-making and prepares learners for careers in data science, finance, healthcare, and technology.

DataMites Institute distinguishes itself by offering a wide array of top IT courses in Pune, including Data Science, Machine Learning, Artificial Intelligence, Python, IoT, data analyst training in Hyderabad and Data Engineering. The institute focuses on hands-on learning, enabling students to gain practical experience through real-world projects, certified internships, and globally recognized certifications accredited by IABAC and NASSCOM FutureSkills, complemented by dedicated placement support.

Providing both classroom and online training, DataMites has built a robust presence across India. From data analyst courses in Pune to centers in Bangalore, Mumbai, Chennai, Ahmedabad, Coimbatore, Hyderabad, Delhi, Jaipur, Kochi, and Kolkata, the institute offers flexible learning options that empower students to acquire industry-ready skills and build successful careers in data analytics.