Bias and Variance TradeOff

Introduction:-

While designing solutions for any business problem with the help of machine learning many challenges are faced like data gathering, cleaning, transformation etc But the most important and critical is prediction errors. Machine learning algorithms aim to learn underlying pattern hidden in the dataset and this can be validated by check performance on the new or test data. Consider a case when solving a classification task, even if we have done a good amount of feature engineering, selection, still the algorithm gives huge misprediction, and the reasons can be that the algorithm selected is not that flexible to get the underlying pattern hidden in the dataset.

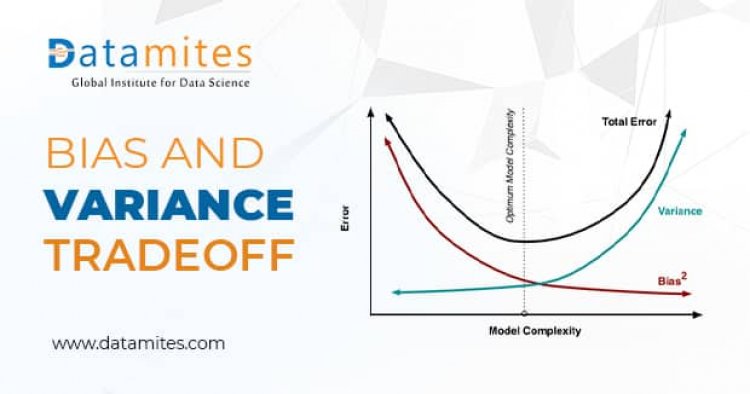
Generally, the error given by an algorithm is summed up as

ERROR=Bias² +Variance +Irreducible Error

Let’s understand each component of the error one by one

Bias = This is simplifying assumptions made by the model to make the target function easier to learn.

Variance = Variance is the amount that estimate of the target function will change if the training data has been changed.

Irreducible Error = This error is native to the algorithm and cannot be reduced.

The goal of any supervised machine learning algorithm is to best estimate the mapping function for the output variable (y) given input data X.Mapping function is the hidden pattern in layman terms to understand.

The equation of the best fit line is called a mapping function.

Let’s see which machine learning algorithms have bias and variance

• Linear algorithms like Linear Regression, Logistic Regression, LDA have high bias making then to learn faster but ultimately low test performance.

• Algorithms like Decision Tree, KNN, SVM have a low bias.

• Linear Regression, Logistic Regression and LDA have low variance.

• Decision Tree, KNN, SVM have high variance.

In short consider bias is an error of training data and variance is an error of test data.

Let’s use train and test error to actually determine the bias and variance of the model.

Case 1 – When train error is 20% and the test error is 19%

Conclusion:- The created model is having high variance and high bias so this is called an under the fitted model.

Case 2 – When the training error is 2% and the test error is 20%

Conclusion:- The model has low bias and high variance. This is the condition of overfitting.

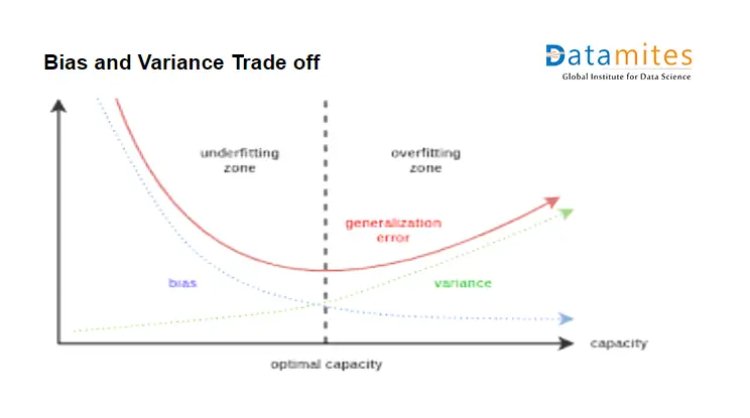
The optimal model should have low training and test error and hence that error is known as generalization error. Ultimately get a model with low bias and low variance.

Model bias and variance can be reduced by hyper tuning the parameters.

RandomForest:- Random Forest is a collection of multiple decision trees coupled parallelly. Decision tree itself has low bias and high variance i.e it will completely fit the training data(low bias ) but if a new test points come the error goes high(high variance). But when multiple decision trees are coupled with row and column sampling the combined variance offered by this collection is low. Hence Random forest is low bias and low variance model.

Boosting algorithms:- The same concept goes with boosting also as they have base learners as DecisionTree only so their aim to reduce the variance. The base learner is weak learners in which the bias is high. Each of these weak learners contributes some vital information for prediction enabling the boosting techniques to produce a strong learner. This stronger learn bring downs the variance.