Understanding Kernel Methods in Machine Learning

Machine learning has evolved to tackle increasingly complex problems, from image recognition and natural language processing to fraud detection and bioinformatics. Many of these tasks involve data that is not linearly separable, making it difficult for traditional algorithms to perform well. This is where kernel methods in machine learning play a transformative role.

Kernel methods provide a mathematical framework to project data into higher-dimensional feature spaces, enabling algorithms to detect patterns and relationships that are otherwise hidden in the original space. These methods are particularly useful in supervised learning, classification, and clustering problems. Their versatility and effectiveness make them a cornerstone in modern artificial intelligence and data science.

In this article, we’ll explore kernel methods in detail, what they are, how the kernel trick works, common kernel functions, key algorithms, real-world applications, and the latest research trends.

What Is the Kernel Trick?

The kernel trick is a mathematical technique that lets algorithms work in high-dimensional spaces without explicitly computing the transformation.

Many machine learning models, such as linear regression or SVMs, rely on finding linear relationships. However, real-world data is often nonlinear, meaning it can’t be separated with a straight line.

To handle this, the data is mapped into a higher-dimensional space where linear separation becomes possible for example, data inseparable in 2D may be separable in 3D. Computing these transformations directly is expensive, but the kernel trick solves this by using kernel functions to calculate inner products as if the data were already transformed.

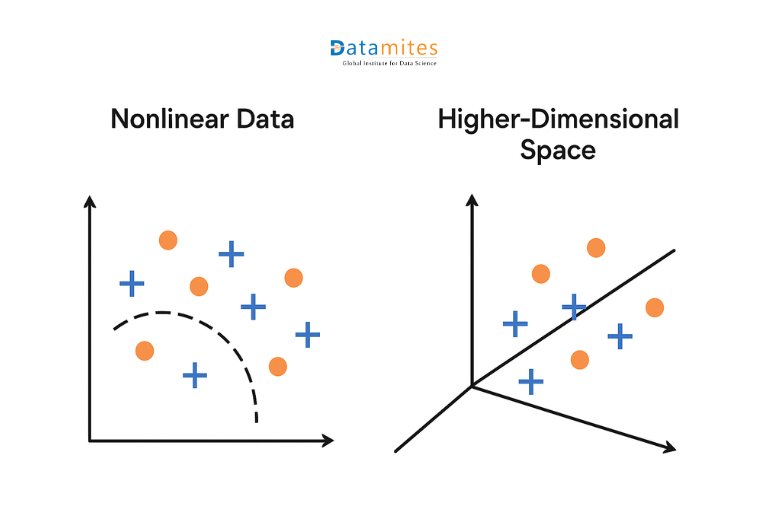
This way, algorithms get the benefits of higher dimensions while still working in the original space saving time and resources.

• Left (Nonlinear Data): Two classes (blue + and orange circles) are mixed in 2D, requiring a curved boundary.
• Right (Higher-Dimensional Space): After mapping to a higher dimension, the classes become linearly separable with a straight line (hyperplane).

The kernel trick enables efficient learning from nonlinear data by making it linearly separable in a transformed space.

Common Kernel Functions

Kernel functions are the backbone of kernel methods. They define the similarity measure between two data points in the transformed feature space. Choosing the right kernel is crucial for the performance of the algorithm. Here are some of the most widely used kernel functions:

1. Linear Kernel

• Simplest kernel function.
• Computes the standard dot product between vectors.
• Useful when data is linearly separable.
• Formula: K(x,y)=xTyK(x, y) = x^T yK(x,y)=xTy

2. Polynomial Kernel

• Captures interactions of features up to a certain degree.
• Can model more complex patterns than the linear kernel.
• Formula: K(x,y)=(xTy+c)dK(x, y) = (x^T y + c)^dK(x,y)=(xTy+c)d
• where ccc is a constant and ddd is the polynomial degree.

3. Radial Basis Function (RBF) or Gaussian Kernel

• Most popular kernel for SVMs.
• Measures similarity based on distance between points.
• Excellent at handling non-linear data.
• Formula:K(x,y)=exp⁡(−∥x−y∥22σ2)K(x,y)=\exp\left(-\frac{\|x-y\|^2 {2\sigma^2}\right)K(x,y)=exp(−2σ2∥x−y∥2​)

4. Sigmoid Kernel

• Inspired by neural networks’ activation functions.
• Can mimic the behavior of a two-layer perceptron.
• Formula: K(x,y)=tanh⁡(αxTy+c)K(x, y) = \tanh(\alpha x^T y + c)K(x,y)=tanh(αxTy+c)

5. Custom Kernels

• Domain-specific kernels are designed for particular tasks (e.g., string kernels for text data, graph kernels for network analysis).
• Provide flexibility to adapt kernel methods to specialized problems.

Choosing the right kernel function is critical. Often, the RBF kernel is a good default choice, but domain-specific kernels can significantly improve performance.

Refer these below articles:

• Genetic Algorithm in Machine Learning
• What is Transfer Learning in Machine Learning?
• How to Learn Machine Learning from Scratch?

Kernel Methods in Machine Learning Algorithms

Kernel functions become powerful when applied to machine learning algorithms. Here are the most common algorithms that benefit from kernelization:

1. Support Vector Machines (SVMs)

Support Vector Machine are the flagship algorithm of kernel methods. With kernels, SVMs can handle complex decision boundaries in high-dimensional spaces. The RBF kernel, in particular, makes SVMs effective in non-linear classification tasks like image recognition and spam filtering.

2. Kernel Principal Component Analysis (KPCA)

While Principal Component Analysis is used for dimensionality reduction, it is inherently linear. Kernel PCA extends PCA by using kernel functions, enabling it to capture non-linear relationships in data. This is particularly useful in pattern recognition and image processing.

3. Kernel Ridge Regression (KRR)

Combines ridge regression with kernels to model non-linear dependencies. It’s widely used for regression problems where the relationship between features and outcomes is not straightforward.

4. Kernel K-Means Clustering

Traditional k-means clustering relies on Euclidean distances, which may not capture complex clusters. Kernel k-means applies kernels to map data into higher dimensions, enabling the detection of non-linear cluster boundaries.

5. Gaussian Processes

A probabilistic approach to regression and classification that heavily relies on kernel functions. Gaussian processes allow flexible modeling of data with uncertainty quantification, making them highly valuable in fields like geostatistics and Bayesian optimization.

Applications of Kernel Methods

Kernel methods are not just theoretical they have extensive applications across industries and research fields:

• Text Classification and NLP: String kernels are effective for sentiment analysis, spam detection, and topic modeling.
• Image Recognition and Computer Vision: SVMs with RBF kernels excel in handwriting recognition, face detection, and object classification.
• Bioinformatics: In healthcare and bioinformatics, kernel methods play a key role in protein structure prediction, gene classification, and medical diagnosis. Today, nearly 60% of healthcare organizations have adopted AI solutions to enhance their operations.
• Finance: Kernel-based regression and classification techniques are widely used in risk modeling, fraud detection, and stock price prediction. With these methods, AI systems can identify fraudulent transactions with accuracy levels of up to 99%.
• Anomaly Detection: Kernels help detect unusual patterns in cybersecurity, manufacturing, and IoT systems.

Kernel methods continue to be highly relevant in addressing real-world machine learning challenges thanks to their ability to manage complex, non-linear relationships. The global chatbot market, valued at USD 5.4 billion in 2023, is expected to surge to USD 15.5 billion by 2028, reflecting a CAGR of 23.3% during this period (Markets and Markets).

Read these below articles:

• Top IT Courses in Belgaum
• Top IT Courses in Jabalpur
• Top IT Courses in Kollam

Recent Advances and Trends in Kernel Methods

Although kernel methods have been part of machine learning for decades, ongoing research continues to expand their scope and relevance. Modern innovations address traditional limitations while combining the strengths of other AI techniques. Below are some of the most notable advances shaping the future of kernel methods:

1. Multiple Kernel Learning (MKL)

Traditional kernel models rely on a single kernel function, such as the RBF or polynomial kernel. However, a single kernel may not capture the full complexity of data in real-world applications. Multiple Kernel Learning (MKL) solves this by combining several kernels, each highlighting different aspects of the data.

• Advantage: By fusing multiple perspectives, MKL produces more robust, accurate, and generalizable models.
• Applications: Bioinformatics (protein function prediction), image recognition, and multimedia classification.

2. Deep Kernel Learning (DKL)

Deep learning is known for its ability to extract hierarchical features, while kernel methods excel at interpretable similarity measures. Deep Kernel Learning (DKL) merges the two: neural networks are used to learn flexible kernel functions that adapt to complex, nonlinear patterns.

• Advantage: This hybrid approach balances deep learning’s representation power with the theoretical foundations and interpretability of kernel methods.
• Applications: Speech recognition, natural language processing, and advanced computer vision tasks.

3. Scalable Kernel Approximations

One of the main challenges with kernel methods is their computational inefficiency on large datasets. Since kernel matrices grow quadratically with the number of data points, training can quickly become impractical. Recent work introduces approximation techniques to make kernel methods scale to big data:

• Random Fourier Features: Approximate kernels by mapping data into a lower-dimensional randomized space.
• Nyström Method: Uses a subset of the data to approximate the full kernel matrix.
• Advantage: These methods reduce computational costs drastically, enabling the use of kernels in real-time applications and big data analytics.

4. Hybrid Models with Kernel Integration

Beyond MKL and DKL, researchers are exploring ways to integrate kernel methods with other machine learning paradigms.

• Kernel + Ensemble Methods: Boosting and bagging combined with kernels improve adaptability and reduce overfitting.
• Kernel + Reinforcement Learning: Kernels help capture non-linear state-action relationships, improving decision-making in robotics and game AI.
• Advantage: These hybrid models deliver greater flexibility, higher accuracy, and better generalization across diverse domains.

Kernel methods are powerful tools for handling non-linear data in machine learning. Using the kernel trick, they allow algorithms to learn complex patterns efficiently without heavy computations. From SVMs to kernel PCA and Gaussian processes, these methods are central to modern AI. With advances in deep and quantum kernel learning, their future looks even brighter. For anyone pursuing Machine Learning courses in Hyderabad, mastering kernel methods is essential.

Known as the country’s “Cyberabad”, the city is home to a thriving IT ecosystem, global tech companies, research institutions, and a growing number of startups leveraging AI and machine learning. For students and professionals, pursuing artificial intelligence courses in hyderabad provides quality training along with access to one of India’s fastest-growing AI job markets.

DataMites Artificial Intelligence Institute in Hyderabad, designed to help learners build the skills required to excel in the fast-growing AI industry. The program is suitable for both beginners and working professionals, with flexible learning modes such as online, classroom, and self-paced options. Accreditations from globally recognized organizations like IABAC and NASSCOM FutureSkills, the certification boosts professional credibility and opens up strong career opportunities in artificial intelligence.