What is a Confusion Matrix in Machine Learning?

There are various ways to check the performance of a machine learning model. One of the most important matrixes is the Confusion Matrix.

Confusion Matrix is used to represent the performance of a classification model. It is also known as the error matrix as it is used to find the errors in the model performance in the form of a matrix.

Here, we are dealing with the binary classification problem i.e. target variable has 2 labels/classes. A confusion matrix can be used for multi-class classification problems also (more than 2 class labels).

For 2 classes, the confusion matrix is represented in a 2 X 2 matrix. Similarly, for 3 classes it can be represented as a 3 X 3 matrix and so on.

The confusion matrix for binary classification is given below:

The matrix is split into two dimensions: – predicted values and actual values. Predicted values are those values, that are predicted by the model, and that have actual values that are the true values for the given observations.

The terminologies used in the matrix are described as

TP – True Positive (When the actual output is 1 and the model predicted 1)
TN – True Negative (When the actual output is 0 and the model also predicted 0)
FP – False Positive (When the actual output is 0 but model predicted 1)
FN – False Negative (When the actual output is 1 but model predicted 0)

Confusion Matrix Machine Learning Foundation

Few Insights from the matrix:

Total Actual: 1 = TP+FN
Total Actual: 0 = FP+TN
Total Predicted: 1 = TP+FP
Total Predicted: 0 = FN+TN
Correctly Predicted: TP + TN
Incorrectly Predicted: FP+FN

Refer this article: Support Vector Machine Algorithm (SVM) – Understanding Kernel Trick

Analogy with statistics: There is the type I errors and type II errors in statistics. Corresponding to true positive and false positive terminology, a type I error follows when you reject the null hypothesis (as false) when it is actually true, which by custom corresponds to a false positive. A type II error happens when you accept the null hypothesis (as true) when it, in reality, is false, which by convention corresponds to a false negative.

Let’s understand this with an example: Suppose, we have blood reports of 100 patients and we have to find out if they are sick or not.

We know that 74 out of 100 are ‘sick’ and 26 out of 100 are ‘not sick’.

But our model predicted that 70 are ‘sick’, out of which 60 are actually ‘sick’ and the rest 10 are ‘not sick’. Our model also predicted 30 as ‘not sick’, out of which 16 are actually ‘not sick’ and 14 are ‘sick’.

Confused!!
Let us create the confusion matrix for this.

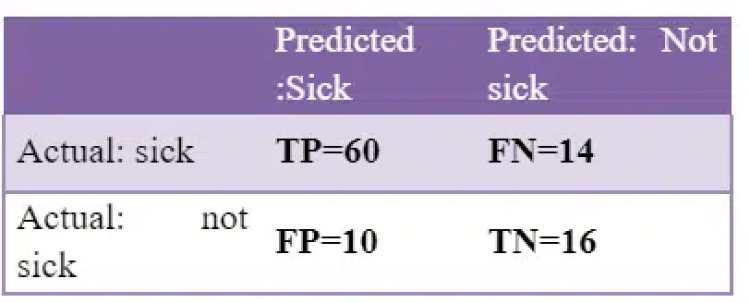
So we can conclude that – Out of a total of 100 predictions,

• Correctly Predicted – 76 (60+16)
• Incorrectly Predicted -24 (10+14)

Read this article: K-Nearest Neighbor (KNN) Algorithm in Machine Learning using Python

We can extract important parameters from the confusion matrix. These are as follows:

1. Accuracy: Number of correct Predictions/Total number of predictions
   Formula: accuracy=TP+TN / (TP + FP+TN+FN)
   =60+16 / 100 = 0.76

2. Precision: It gives answer to the question: Out of total predicted positive results, how many results were actually positive?
Formula: precision = TP / (TP + FP)
= 60 / (60 + 10) = 60 / 70 = 0.857

3. Recall: It gives answer to the question: Out of total actual positive values, how many positives were predicted correctly.
Formula: recall = TP / (TP + FN)
= 60 / (60 + 14) = 60 / 74 = 0.811

4. F1 score: It is weighted average of precision and recall.
Formula: F1 score= 2(PrecisionRecall) / (Precision + Recall)
= (20.850.81)/(0.85+0.81) = 0.829

Also read: A Guide to Principal Component Analysis (PCA) for Machine Learning

When to use Accuracy, Precision, Recall and F1 score?

• Accuracy: When you have Balanced Dataset
• Precision and Recall: It depends on problem statement. When FP is important, use precision and when FN is important, use Recall
• F1 Score: When precision and recall both are important

Confusion Matrix In Machine Learning

Additional Information:

• TP and TN should be high
• FP and FN should be low
• Recall is also known as TPR- True Positive Rate (also known as sensitivity)

Being a prominent data science institute, DataMites provides specialized training in topics including machine learning, deep learning, artificial intelligence, the internet of things, and python Courses. DataMites have been authorized by the International Association for Business Analytics Certification (IABAC), a body with a strong reputation and high appreciation in the analytics field.

ROC Curve and AUC Score