Logistic Regression with Example

Logistic Regression is a Supervised Machine Learning Algorithm utilized for classification.

Examples for classification include: Email spam or ham, will buy or not buy a product, disease predictions such as cancerous or noncancerous cells.

Logistic regression is a Probability problem. Meaning that the outcome of the algorithm is between 0 and 1. It maintains a threshold value to classify the data points(samples). The probability value above the threshold is evaluated to true, otherwise to false.

The logistic regression is based on the Linear Regression i.e it is derived from the Linear Regression. To understand how this probabilistic algorithm is based on Linear Regression. Let us take an example and derive the Logistic Regression equation.

Problem: the probability of being infected given the range of age (20 to 50)

Let us try to solve this problem using Linear Regression initially

Given age= 20 between 55

Note: 0<=p<=1

//The probability value should range from 0 to 1.

We have 0<=p<=y= β0 + β1*X1 // linear regression equation1

Case 1: β0 =-1.700, β1 =0.064, age=35 //β0is the y-intercept and β1 is the slope of the straight line drawn. Β0 and β1 are randomly chosen.

Let us try to plug in the values to the straight-line equation we have and observe the corresponding results.

y(p=1|age)=-1.700+0.066(35) = 0.54

Case 2: for age 25 and 45

y(p=1|age)=-1.700+0.064(25)= -0.09 //negative result

y(p=1|age)=-1.700+0.064(45)= 1.20 //value is more than 1

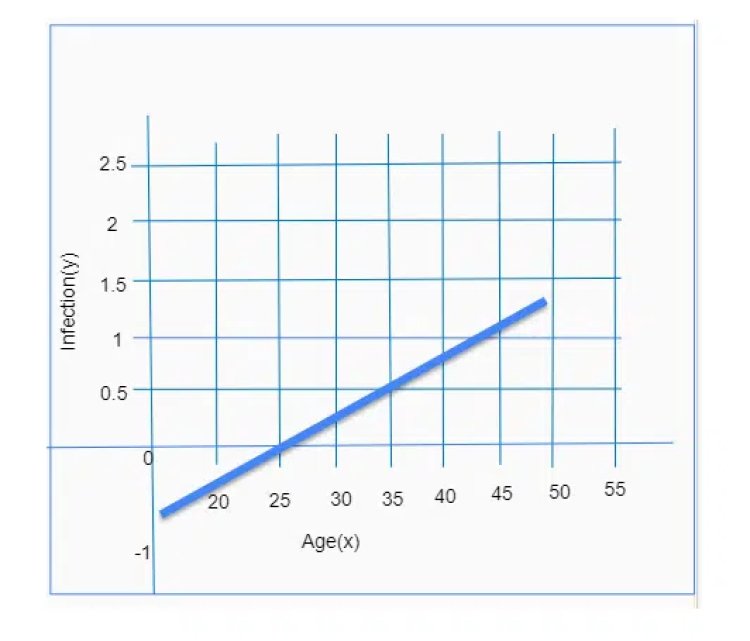
We have noticed that, for the age 25, the final value of the equation is less than 0 and for the age 45, the final value of the equation is greater than 1.

According to the Logistic Regression assumption, the values should range from 0 to 1. Thus, trying to solve this problem using linear regression is failing to satisfy the assumptions of logistic regression.

The corresponding plotting is shown below.

Now let us try to solve the same problem using logistic regression

The probability value should be greater than or equal to 0

For P>=0

P(X)= exp(β0 + β1*X)

// taking exponentiation to the straight-line equation will give us the positive value.

For P<=1
// the probability value should be less than or equal to 1.

P(X)= exp(β0 + β1X)/1+exp(β0 + β1X) //dividing a number by one number greater than that will give us the value below the numerator value.

This equation is referred to as the Logistic Regression equation.

P(X)(1+exp(β0 + β1X)=exp(β0 + β1X)

P(X)= exp(β0 + β1X)-p(x) exp(β0 + β1X)

P(X)= (1-P(X)) exp(β0 + β1*X)

P(X)/1-P(X)= exp(β0 + β1*X)

Take nat. log on both sides

Ln(P/1-P)= β0 + β1*X //exponent gets canceled after applying nat. Log. this function is referred to as the logit function

The right-hand side of the equation is equal to the straight-line equation. Which is equal to Y= β0 + β1*X. Hence, logistic regression is based on linear regression.

Going back to the equation below.

P(x)= exp(β0 + β1X)/1+exp(β0 + β1X)

Divide both numerator and denominator by exp(β0 + β1*X)

Therefore we get, P(X) = 1/1+exp(- β0 + β1*X)

Sometimes written as P(x)=1/1+exp(-z) referred to as sigmoid equation where z= β0 + β1*X

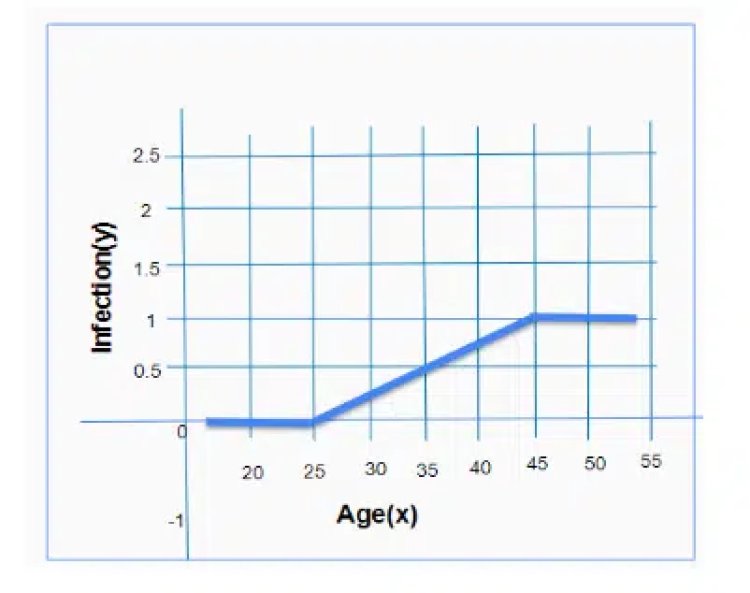
As it can be noticed, the values are ranging from 0 to 1, which satisfies logistic regression assumptions.
The final plot is shown. The curve is also referred to as s- curve or Sigmoid curve.

DataMites provides data science, artificial intelligence, machine learning, python, deep learning courses. The courses are accredited by IABAC®.